一定の速さでまっすぐ進んで壁にぶつかる絵ばかり描いているわけにもいかないので、もう少し違う動きも表現してみよう。ここでは振動・回転・渦などを表現するが、そのためには三角関数の知識が必要となる。
三角関数なんか見たくもないという人も多いかもしれないが、避けて通れないので、あきらめよう。通り一遍の最小限の知識だけ身につけることにする。
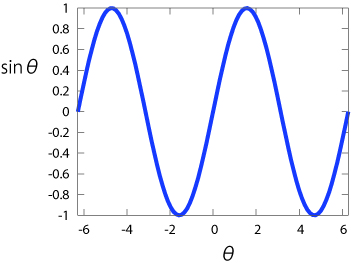
三角関数というのは、振動を表す関数だと思っておけばいい。たとえば、sin という関数の絵を描くと下のようになる。

θという変数にひとつ値を与えると、関数の値 sinθ が決まる。見てわかるように sin は -1 と 1 のあいだを周期的に振動する関数である。θがπ(つまり、約3.14)の倍数のときに sinθ は 0 になり、振動の周期は 2π である。
これを使って、円が横に振動するアニメーションを作ってみると、たとえば
float theta;
int r;
void setup()
{
theta = 0;
r = 30;
noStroke();
}
void draw()
{
float x;
background(0);
theta += 0.1;
x = r*sin(theta);
ellipse(x+50,50,30,30);
}
のようになる。ここでは、アニメーションの1ステップごとに変数thetaを0.1ずつ増やしている。変数thetaはintではなくfloat とすることに注意。rはintにしてあるが、これはどちらでもよい。このプログラムではxは -r と r のあいだで振動する。
なお、theta と r は setup より前に宣言しなくてはならないが、x は draw の中だけで使うので、draw の中で宣言している。今の場合は、一番上で r や theta と一緒に宣言してもよい。
もうひとつの三角関数cosとの関係は次の図を見ればよい
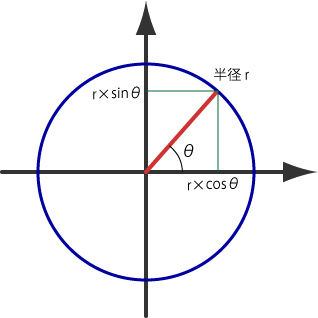
半径 r の円上の一点に中心から直線を引いたとき、直線とx軸とのあいだの角度をθとすると、 円上の点の座標は (r×cosθ, r×sinθ) になる。これを使って、中心のまわりで円をぐるぐる回すプログラムを書くとつぎのようになる
float theta;
int r;
void setup()
{
theta = 0;
r = 30;
noStroke();
}
void draw()
{
float x,y;
background(0);
theta += 0.1;
x = r*cos(theta);
y = r*sin(theta);
ellipse(x+50,y+50,30,30);
}
このプログラムではthetaを0.05ずつ増やしている。
半径 r の円上の一点に中心から直線を引き、直線とx軸とのあいだの角度が theta のとき、 円上の点の座標はこうなる
渦巻きも描いてみよう。渦はだんだん半径を大きく(あるいは、小さく)しながら円運動させればよいから、r も少しずつ増やせばよい。以下は、少し大きいウィンドウにして、渦巻き状に円を動かすプログラムである。
float theta;
float r;
void setup()
{
size(300,300);
theta = 0;
r = 0;
noStroke();
}
void draw()
{
int j;
float x,y;
background(0);
theta += 0.05;
r += 0.1;
if (r>150){r = 0;}
x = r*cos(theta);
y = r*sin(theta);
ellipse(x+150,y+150,30,30);
}
ここでは r が150に達したら、半径を0に戻すように if (r>150){r = 0;} という文をいれている
長方形が周期的に伸び縮みするアニメーション。 円の半径が周期的に変わるアニメーション。 色が周期的に変わるアニメーション。